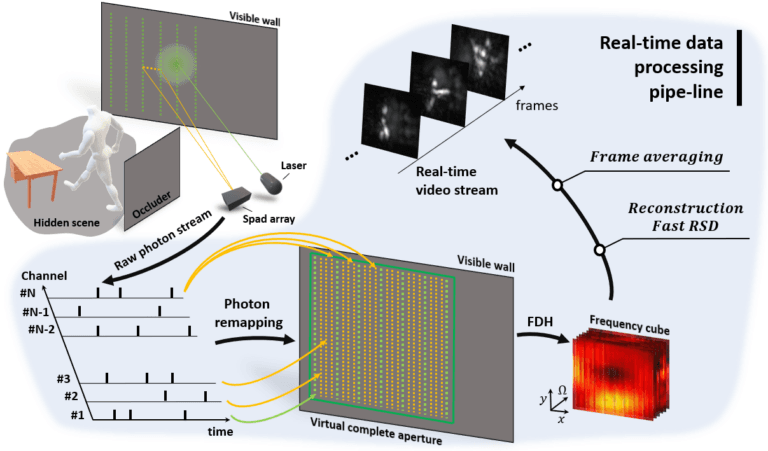
Non-line-of-sight (NLOS) imaging allows to observe objects partially or fully occluded from direct view, by analyzing indirect diffuse reflections off a secondary relay surface. Despite its many potential applications, existing methods lack practical usability due to several shared limitations, including the assumption of single scattering only, lack of occlusions, and Lambertian reflectance. Line-of-sight (LOS) imaging systems, on the other hand, can address these and other imaging challenges despite relying on the mathematically simple processes of linear diffractive wave propagation. In this work we show that the NLOS imaging problem can also be formulated as a diffractive wave propagation problem. This allows to image NLOS scenes from raw time-of-flight data by applying the mathematical operators that model wave propagation inside a conventional line-of-sight imaging system. By doing this, we have developed a method that yields a new class of imaging algorithms mimicking the various capabilities of LOS cameras. To demonstrate our method, we derive three imaging algorithms, each with its own unique novel capabilities, modeled after three different LOS imaging systems. These algorithms rely on solving a wave diffraction integral, namely the Rayleigh-Sommerfeld Diffraction (RSD) integral. Fast solutions to RSD and its approximations are readily available, directly benefiting our method. We demonstrate, for the first time, NLOS imaging of complex scenes with strong multiple scattering and ambient light, arbitrary materials, large depth range, and occlusions. Our method handles these challenging cases without explicitly developing a light transport model. We believe that our approach will help unlock the potential of NLOS imaging, and the development of novel applications not restricted to laboratory conditions, as shown in our results.
Measurement and phasor field on the scanning wall. The image on the left side shows the hardware scanning. The right image shows the virtual phasor field of the hidden scene (Global and Local display range for each frame). Notice that this raw virtual phasor field wavefront contains the direct and indirect signal of the hidden scene, interestingly we can also notice the shadow of the chair at around Time index:800.
| Virtual transient camera. Finally, the hidden image is decoded by using the diffraction theory. Moreover, we can build the virtual camera only see the direct signal in the hidden scene. |
| Virtual regular camera using the inverse diffraction. We can also build the virtual regular camera by using the standard inverse diffraction. The image on the left shows the inverse diffraction by choosing Φ operator. Examples are shown on the right, refocusing results are calculated from the Rayleigh-Sommerfeld Diffraction (RSD) (top) and Fresnel Diffraction (bottoms). |
Robustness of our technique. a. Reconstruction in the presence of strong ambient illumination (all the lights on during capture). b. Hidden scene with a large depth range, leading to very weak signals from objects farther away.